Week 10 Problems
These problems are taken from the Chapter 12 Problems in the text on page 155, with some modifications.
-
(Problem 7) Prove that ${(2,1),(1,1)}$ and ${(12,5),(7,3)}$ are bases for the same lattice.
-
(Problem 8) Let $G$ be a subgroup of $E(n)$ and let $H$ be the translation subgroup of $G$ – that is, the intersection of $G$ with the translation subgroup of $E(n)$. Prove that $H$ is normal in $G$ and that $G/H$ is isomorphic to a subgroup of $O(n)$.
-
(Problem 12) Prove or disprove: an element of $E(2)$ of the form $(A,x)$ with $x\not=0$ is of infinite order.
-
(Problem 15) Let $G$ be a group with a subgroup $H$ (not necessarily normal) and a normal subgroup $N$. $G$ is a semi-direct product of $N$ by $H$ is $H\cap N$ is the trivial group and $HN=G$. Prove that
-
$S_{3}$ is the semidirect product of $A_{3}$ by $H$, where $H$ is generated by a transposition.
-
Prove that the dihedral group is the semidirect product of the rotation subgroup by the group generated by a reflection.
-
Prove that the Quaternion group is not a semidirect product.
For the next two problems you can refer to the table in the text (Table 12.23) or this table from Schattenschneider, The Plane Symmetry Groups: Their Recognition and Notation, American Math Monthly 1978.
-
-
(Problem 16) Which of the 17 wallpaper groups preserves the symmetry of this pattern:

-
(Problem 17) Which of 17 wallpaper groups preserves the symmetry of this pattern:

-
This problem is not from the text. Schattenschneider claims that this pattern has symmetry group pmm.
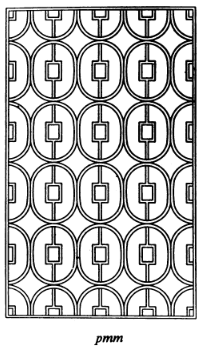
Her diagram for this symmetry is here:
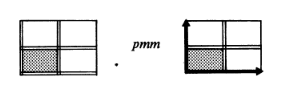
-
Draw the translation lattice on the image.
-
Draw the reflection axes.
-
Find generators and relations for this symmetry group.
-
-
This problem is not from the text. Let $H$ be the set of matrices in $h\in \mathrm{GL}_{n+1}(\mathbb{R})$ with block form: \(h=\left(\begin{matrix} A & \Bigg\vert & \begin{matrix} a_1 \\ \vdots \\ a_n \end{matrix}\\ \hline \begin{matrix} 0 &\cdots & 0 \\ \end{matrix} &\vert &1\\ \end{matrix}\right)\)
where $A$ is an orthogonal matrix.
-
Prove that $H$ is a subgroup.
-
Let $(A,a)$ be an element of $E(n)$, so $A$ is an $n\times n$ orthogonal matrix and $a=(a_1,\ldots, a_n)$ is an element of $\mathbb{R}^{n}$. Define a map \(f:E(n)\to H\) by \(f((A,a))= \left(\begin{matrix} A & \Bigg\vert & \begin{matrix} a_1 \\ \vdots \\ a_n \end{matrix}\\ \hline \begin{matrix} 0 &\cdots & 0 \\ \end{matrix} &\vert &1\\ \end{matrix}\right)\) Prove that this is an isomorphism.