Vantage Point Trees

A vantage point tree is a data structure designed to efficiently search for the point (or the n points) in a metric space X that is/are closest to a given point P. The original idea seems to be due to Jeffrey Uhlmann, who described them in the (very short) paper Metric Trees, published in Applied Mathematics Letters, Volume 4, Issue 5, in 1991. The structure was named by Peter Yianilos in his paper Data Structures and Algorithms for Nearest Neighbor Search in General Metric Spaces.

Uhlmann’s brief description of how to construct a vantage point tree is as follows. Given a non-empty set X of points in a metric space with metric $d(\cdot, \cdot)$, proceed as follows:

1. Select a point $x_0$ from $X$.
2. Compute the median $m$ of the set of distances ${d(x,x_0): x\in X-{x_0}}$ and split the set $X-{x_0}$ into $X_L$ and $X_R$, where $X_L$ consists of the points closer than $m$ to $x_0$ and $X_R$ the rest. Recursively construct the left and right subtrees of the desired tree rooted at $x_0$ from $X_L$ and $X_R$ respectively. For each node, record the associated median distance that splits the left and right subtrees.

Constructing the tree is clearly an $O(n\log n)$ algorithm.

Given a point $p$, we can use the resulting tree to find the point in $X$ that is closest to $p$ as follows.

Start at the root node and compute the distance from the root to $p$. Then proceed through the tree as follows; at each node $n$ we have the distance $d$ from the point $p$ to $n$. We also have the closest node we’ve found so far ($n_0$), and the distance to that node ($d_0$). Finally, we have the median distance $m$ that splits the left and right subtrees at $n$.

First, we make the following two observations, which are applications of the triangle inequality:

1. The nearest point to the node $n$ in the right subtree is $m$. So if the true closest point to $p$ is in the right subtree, it must be the case that $d\ge m-d_0$.
2. If the true closest point to $p$ is in the left subtree, then it must be the case that $d\le m+d_0$.

Thus we have three cases to consider:

1. $d<m-d_0$. In this case, the true closest point must be in the left subtree, so we continue our search with that subtree.
2. $d>m+d_0$. In this case, the true closest point must be in the right subtree, so we continue our search there.
3. $m-d_0\le d \le m+d_0$. In this case, we can’t be sure which subtree contains the desired point, so we have to look in both subtrees.

If it weren’t for case 3, the algorithm to find the closest point would be clearly $O(\log n)$.

There are many implementations of this algorithm available on github. My implementation is available as a gist here..

Experiments comparing my implementation with the the method of using the numpy sort algorithm to pick out the closest points shows that my implementation does better on large sets of points (not counting the time to build the tree).
On 100000 points, the sort-based algorithm is about 20 times faster than the vptree implementation. On 10000000 points, the vptree is 40 times faster.

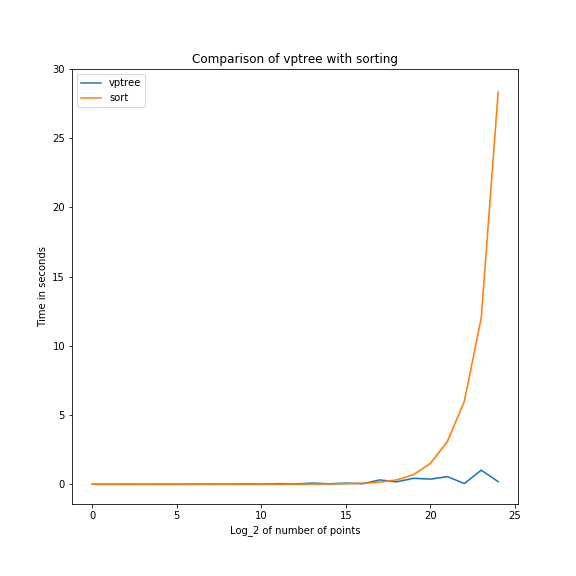
The vptree time is more variable than the sort-based time, because the speed depends on how often you can take only one of the two branches in the tree, and that depends on the distribution of the points.