Week 12 Problems
These problems are taken from the Chapter 14 problems of the text.
-
(Problem 5). Let $G=A_4$. Let $G$ act on itself by conjugation. Find the orbits (conjugacy classes) of $G$ and, for each class, the stabilizer of an element in that class. Verify the class equation.
-
(Problem 2b). Let $X={1,2,3,4,5,6}$ and $G$ be the group consisting of the permutations \((1),(12),(345),(354),(12)(345),(12)(354)\). (Note that $G$ is the product of \(\mathbb{Z}_{2}\) and \(\mathbb{Z}_{3}\) with the first component acting on $[1,2]$ and the second on $[3,4,5]$. Find $X_g$ and $G_x$ for each $x\in X$ and $g\in G$.
-
Let $X$ be a set with a $G$ action and $Y$ be a set with $H$ action. Prove that the formula $(g,h)\cdot(x,y)=(gx,hy)$ is an action of $G\times H$ on $X\times Y$. Prove that the stabilizer of $(x,y)$ is $G_x\times H_y$ for any $x\in X$ and $y\in Y$.
-
(Problem 9) How many ways (up to symmetry) can you color the vertices of an equilateral triangle with 3 colors?
-
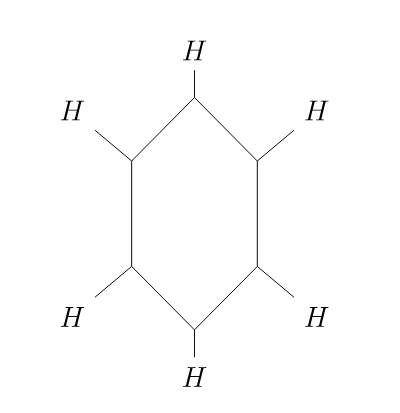
(Problem 16). A molecule of benzene is made up of six carbon atoms and six hydrogen atoms arranged in a hexagonal shape as shown at the end of this assignment.
a. How many different compounds can be formed by replacing one or more of the hydrogen atoms with a chlorine atom?
b. How many different compounds can be formed by replacing 3 of the six hydrogen atoms with a CH_3 radical?
-
Let $X$ be the set of words made up of the three letters $A,B,C$ of length 6. What are the orbits of $S_6$ acting on $X$ by permuting the position of the letters? For example the transposition $(12)$ interchanges the letters in positions 1 and 2 of the word.