Sequences

Definition: An (infinite) sequence with rational coefficients is a function \(a:\mathbb{P}\to\mathbb{Q}\). Normally we view it as the sequence \(a(1),a(2),\ldots\).

Some examples:

• \(a(n)=0\) for all \(n\) (the zero sequence).
• \(a(n)=1/n\) for \(n=1,2,\ldots\)
• \(a(n)=n\) for \(n=1,2,\ldots\)
• \(a(n)=(-1)^n\) for \(n=1,2,\ldots\)

We would like to have a way to speak about what happens to sequences as \(n\) gets larger and larger (so for example the sequence grows, it bounces around, or it approaches a particular number.)

Limit of a sequence

Definition: Let \(a(n)\) be a sequence. Then we say that the limit of \(a(n)\) is \(L\) if, for every \(\epsilon>0\), there is an integer \(N\), so that \(|a(n)-L|<\epsilon\) for all \(n\ge N\). This is written:

\[ \lim_{n\to\infty} a(n)=L. \]

and we say that the sequence converges to \(L\).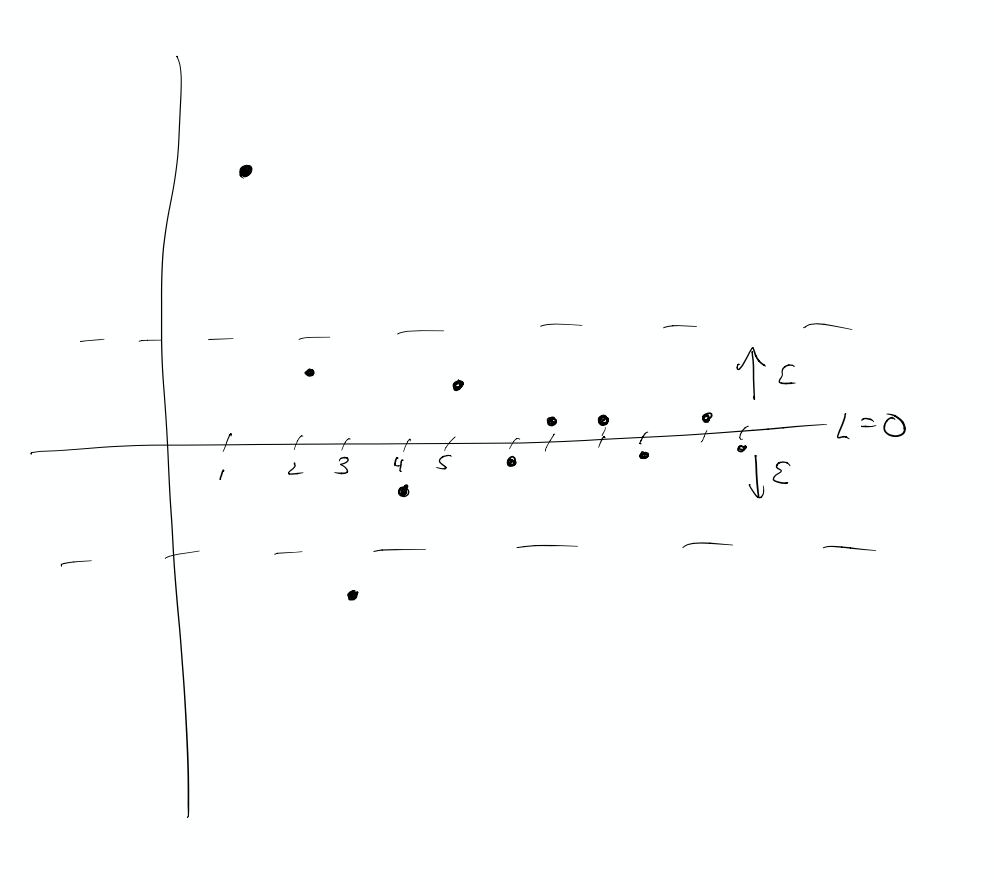

Limits are about estimation

Examples

• Let \(a(n)\) be the sequence defined by \(a(1)=1, a(2)=1/2, and a(n)=0\) for \(n>2\). Prove that the limit \(\lim_{n\to\infty} a(n)=0\).
• Let \(a(n)\) be the sequence \(a(n)=1/n\). Prove that the limit of \(a(n)\) as \(n\to\infty\) is zero.
• Let \(a(n)=(-1)^{n}\). Prove that the limit isn’t \(1\). Then prove there is no limit.
• Let \(a(n)=n\). Is there a limit?
• Let \(a(n)=(n+1)/n\). Prove that the limit is \(1\).
• Let \(a(n)=4+(-1/2)^{n}\).

Non-convergence

A sequence \(a(n)\) does not converge to a limit \(L\) means that - there exists \(\epsilon>0\) such that - for all \(N\) - there exists \(n\ge N\) such that - \(|a(n)-L|>\epsilon\)

The sequence \(a(n)=(-1)^{n-1}\) does not converge to any limit because no matter what \(L\) you pick and what \(N\) you choose the distance \(|(-1)^{n-1}-L|\) bounces back and forth between \(|1-L|\) and \(|1+L|\) so if you choose \(\epsilon\) smaller than the maximum of these two you satisfy the ‘non-convergence’ requirement.

Limit rules make arguments standard

Proposition: If \(a(n)\) converges to \(L\) and \(b(n)\) converges to \(M\) then \(a(n)+b(n)\) converges to \(L+M\).

Proof: The estimation side calculation is that we can choose \(N\) large enough that \(|a(n)-L|<\epsilon\) and \(|b(n)-M|<\epsilon\) for \(n\ge N\). Then \(|a(n)+b(n)-L-M|<2\epsilon\). So given \(\epsilon\) we should choose \(N\) large enought that \(|a(n)-L|<\epsilon/2\) and similarly \(|b(n)-M|<\epsilon/2\).

Proposition: Suppose that \(a(n)\) is a sequence converging to \(L\). Prove that there is an \(N\) so that \(|a(n)|<2L\) for \(n\ge N\).

Proof: Choose \(\epsilon=L/2\). Then there is an integer \(N\) such that \(|a(n)-L|<L/2\) for all \(n\ge N\). This means that \(a(n)\) is between \(L/2\) and \(3L/2\) so in particular it is less than \(2L\).

Proposition: Suppose that \(a(n)\) converges to \(L\). Prove that \(a(n)^2\) converges to \(L^2\).

Proof: \(|a(n)^2-L^2|=|a(n)^2-a(n)L+a(n)L-L^2|\le |a(n)||a(n)-L| + |L||a(n)-L|\). We can choose \(N\) so that \(|a(n)|<2L\) and \(N'\) so that \(|a(n)-L|<\epsilon/4L\). Then for \(n\) bigger than both of these we have \[|a(n)||a(n)-L|+|L||a(n)-L|\le (2L)\epsilon/4L+L\epsilon/4L=\epsilon/2+\epsilon/4=3\epsilon/4<\epsilon.\] Thus for \(n\ge\mathrm{max}(N,N')\) we have \(|a(n)^2-L^2|<\epsilon.\)